Arbres¶
Nous avons vu les structures de données linéaires : notamment les piles et les files. Désormais, nous allons étudier une structure plus complexe où les données sont organisées de manière hiérarchique. Cette structure est extrêmement utilisée en informatique et dans d'autres domaines (en biologie par exemple).
Exemples¶
- Les arbres généalogiques
- Les arborescences de fichiers
- Les arbres de probabilités
En informatique :
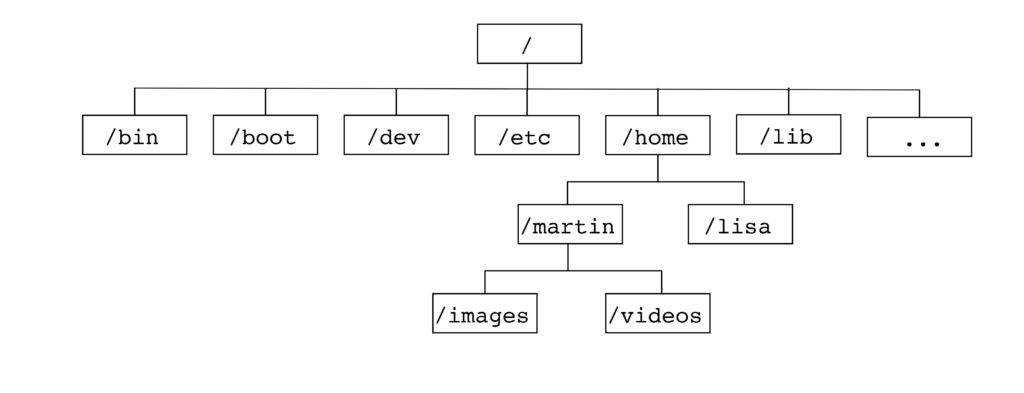
En biologie :
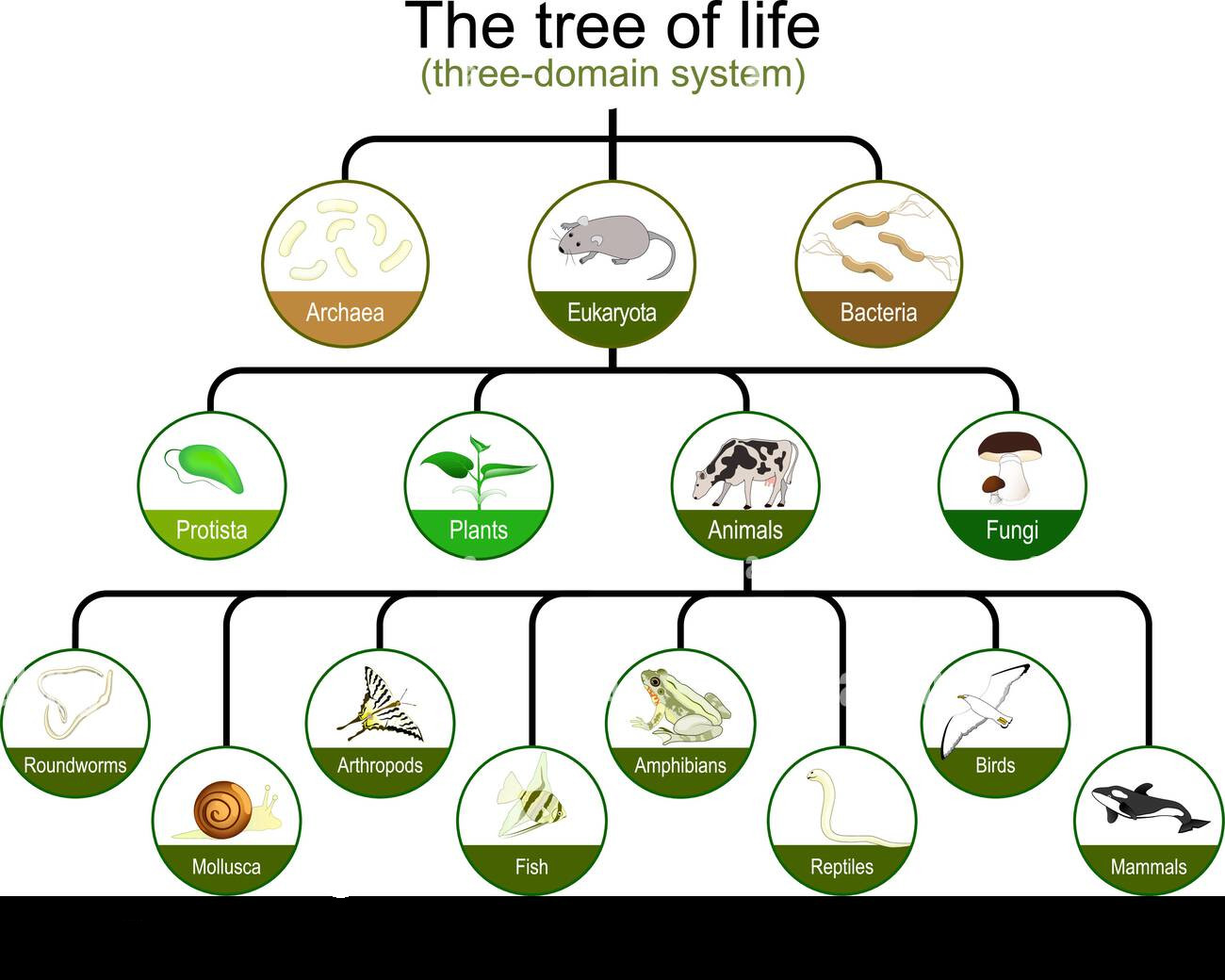
Les arbres sont des structures de données très utilisées en informatique ; on peut citer par exemple l'évaluation d'expressions arithmétiques, l'analyse syntaxique (théorie des langages), compilation d'un programme, prise de décision (machine learning),etc. La liste est très longue...
De plus, les structures de données déjà vues, notamment les listes, ne permettent pas de traduire correctement cette structure hiérarchique. Par contre, un arbre permet de représenter des données présentes dans une liste de manière linéaire, on peut donc voir un arbre comme une généralisation d’une liste.
Nous n'avons pas encore vu les graphes en NSI, mais vous êtes censés les avoir éthudiés en SNT. Nous pouvons dire qu'un arbre est un graphe particulier.
Définition
Un arbre est un graphe acyclique et connexe.
Cette définition peut sembler complexe à première vue, mais elle est en fait très intuitive.
Graphe connexe et non connexe :

Exemples de graphes cycliques :

Un ensemble d'arbres est appelé forêt, par exemple :
Exercices
Dire si les graphes ci dessous sont des arbres ou pas
a)
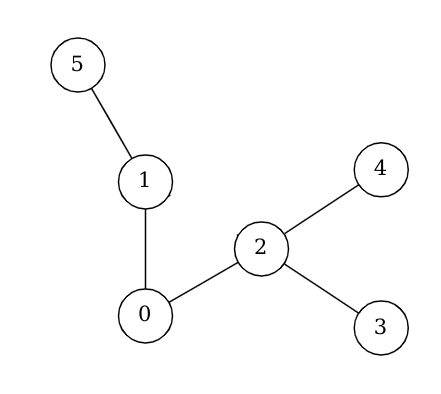
b)

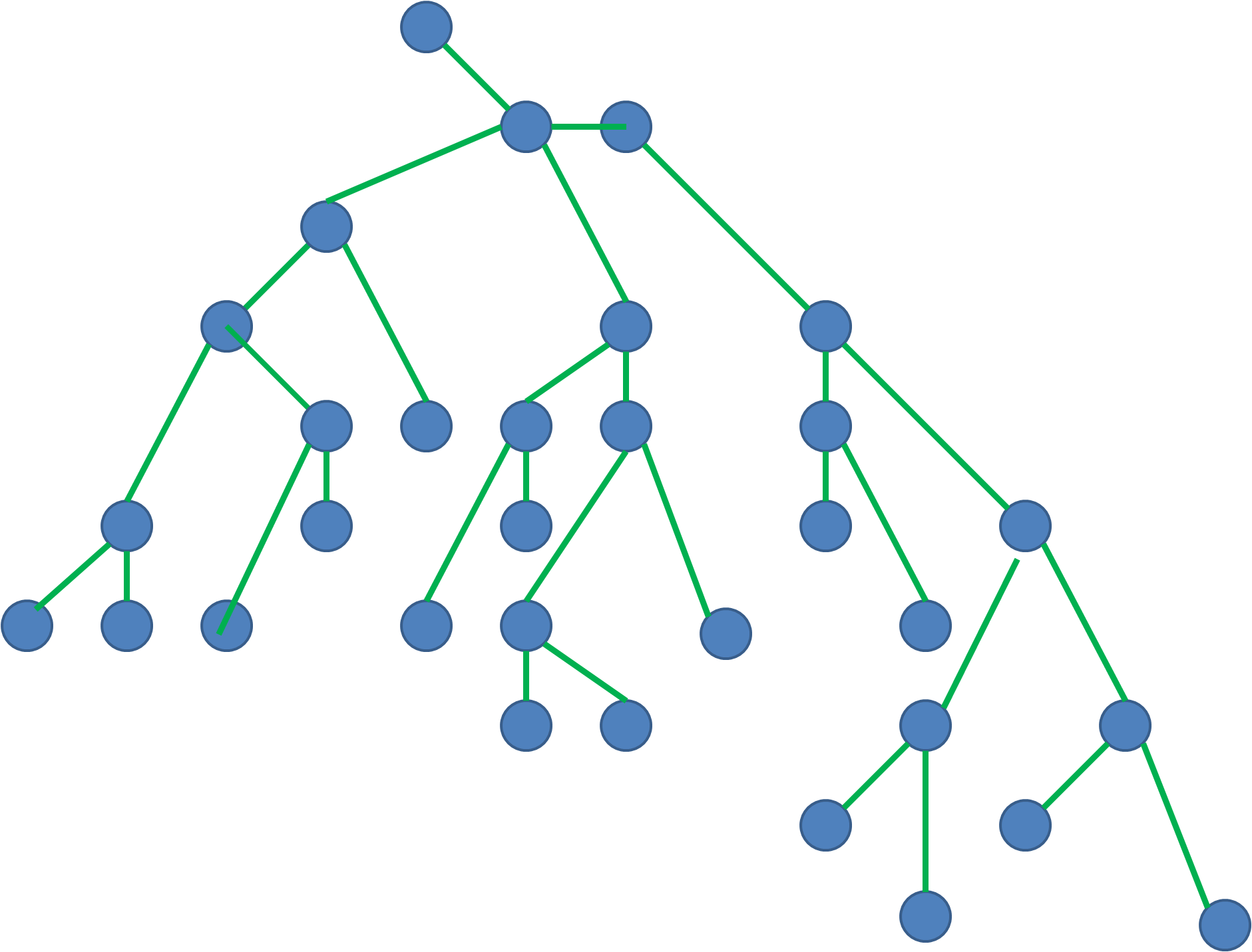
d)
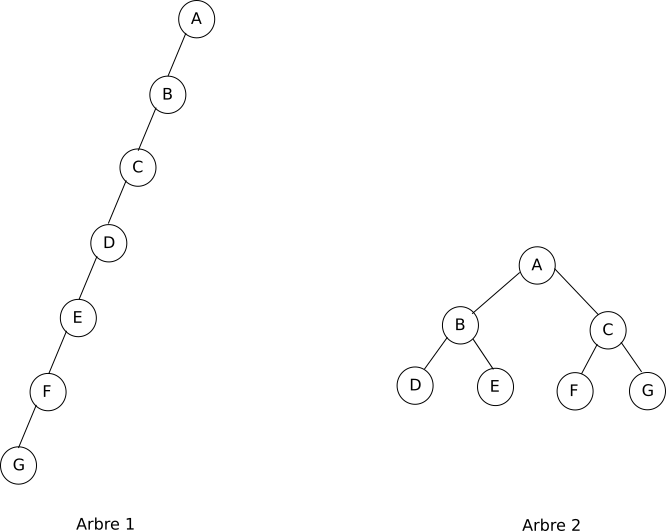
On a l’habitude, lorsqu’on dessine un arbre, de le représenter avec la tête en bas, c’est-à-dire que la racine est tout en haut, et les nœuds enfants sont représentés en-dessous du nœud parent.
Définition récursive
Un arbre est soit vide, soit composé d’un élément (la racine) et d’une liste d’arbres (les sous-arbres).
Terminologie¶
Caractéristiques d’un nœud :
- Noeud : racine d’un sous-arbre
- Profondeur : longueur du chemin depuis la racine
- Feuille :nœud dont les sous-arbres sont vides
Caractéristiques d’un arbre :
- Arité : nombre maximal d’enfants
- Hauteur : valeur maximale de la profondeur
- Taille : nombre total de nœuds
Remarque sur la hauteur
Il n’existe pas de définition universelle pour la hauteur d’un arbre et la profondeur d’un nœud dans un arbre. La profondeur de la racine peut être de 1 ou de 0. Dans ce cours elle vaudra 0, mais il faut bien lire l'énoncé pour connaître quelle est la valeur de la profondeur de la racine.
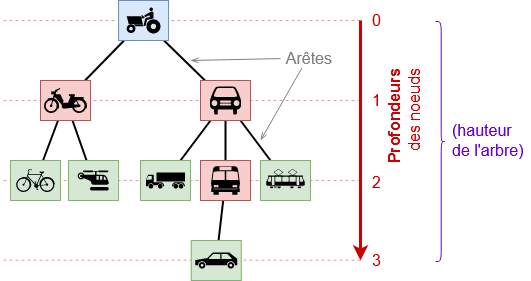
Terminologie « généalogique » :
- Père, parent, ...
- Fils, enfant, ...
- Frère
La racine de l’arbre est l’unique nœud ne possédant pas de parent.
Exercice
Soit l'arbre

Déterminer :
a. Les feuilles
b. Son arité
c. Sa hauteur
d. Sa taille
Arbres particuliers¶
Arbre filiforme
Tout nœud qui n’est pas une feuille a exactement un enfant.
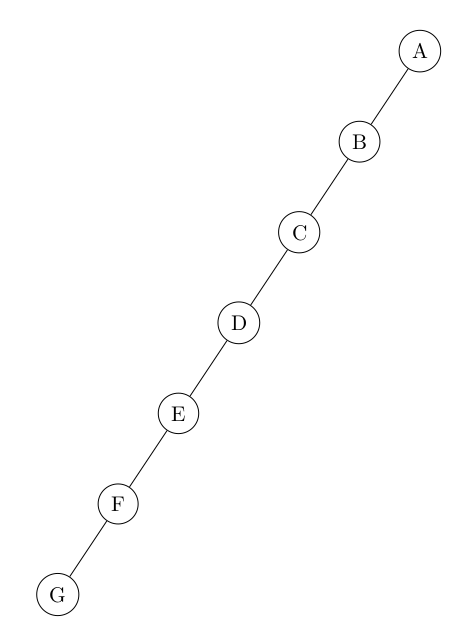
On retrouve ici la structure linéaire abstraite liste.
Soit A un arbre filiforme (aussi appelé arbre dégénéré), de hauteur \(ℎ\) et de taille \(\tau\). On a alors \(h\) = \(\tau\) - 1.
Question
Quel peut être l'arité d'un arbre filiforme ?
Arbre d’arité n complet
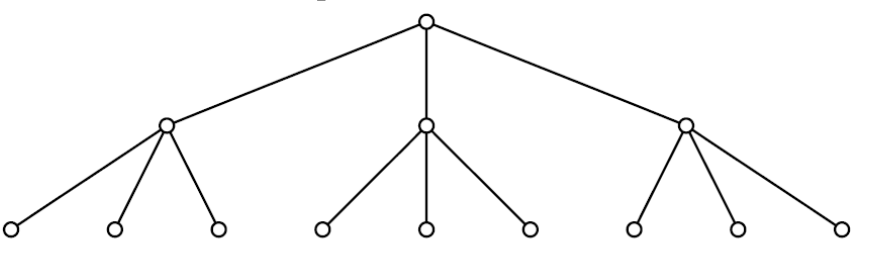
- Quel est l'arité de cet arbre ?
Soit A un arbre complet d’arité \(n\), de hauteur \(h\) et de taille \(\tau\). On a alors \(\large \tau = \Sigma_{i=0}^{h} n^{i} = ...\)
- Finir ce calcul